第二章 相交与平行线
1. 两条直线的位置关系
同一平面内,两条直线的位置关系:要么相交,要么平行。
(1)相交
定义 :同一平面内,若两条直线只有一个公共点,则这两条直线为相交线。
(2)平行
定义 :在同一平面内,不相交的两条直线叫做平行线。

2. 直线的相交
(1)两线四角
①对顶角
定义 :两个角有公共顶点0,两个角的两边互为反向延长线;具有这种位置关系的两个角叫做对顶角。
性质 :对顶角相等
注意 :互为对顶角的两个角一定相等,但两个角相等不一定互为对顶角。
②互补角
定义 :如果两个角的和是180°,那么称这两个角互为补角。
性质 :同角或等角的补角相等。
注意 :互为领补角的两个角一定互补,但两个角互补不一定互为领补角(领补角:相邻的两个互补角)。
拓展:互余角
定义 :如果两个角的和是90°,那么称这两个角互为余角。
性质 :同角或等角的余角相等。
(2)垂直
定义 :两条直线相交成四个角,如果有一个角是直角,那么称这两条直线互相垂直。
垂线 定义 :其中一条直线叫另一条直线的垂线。
垂足 定义 :它们的交点叫做垂足。
符号 :⊥
性质 :1、平面内,过一点有且只有一条直线与已知直线垂直。
2、直线外一点与直线上各点连接的所有线段中,垂线段最短。
直线的距离 定义 :直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
3. 直线的平行
(1)三线八角
①同位角
定义 :两条直线被第三条直线所截,位置相同的一对角(即两个角分别在两条直线的同一侧,并且在第三条直线的同侧),叫做同位角。
②内错角
定义 :两条直线被第三条直线所截,两个角都在两条直线之间,并且位置交错的一对角(即两个角分别在第三条直线的两侧),叫做内错角。
③同旁内角
定义 :两条直线被第三条直线所截,两个角都在两条直线之间,并且在第三条直线的同侧的一对角,叫做同旁内角。
(2)平行线
定义 :在同一平面内,永不相交的两条直线称为平行线。
符号 :∥(a平行于b,记作a∥b)
公理 :经过直线外一点,有且只有一条直线与这条直线平行。
公理推论 :如果两条直线都和第三条直线平行,那么这两条直线也互相平行;即:平行于同一条直线的两条直线平行。
性质 :①两条直线平行,同位角相等。
②两条直线平行,内错角相等。
③两条直线平行,同旁内角互补。
判定 :①同位角相等,则两条直线平行。
②内错角相等,则两条直线平行。
③同旁内角互补,则两条直线平行。
平行线的证明方法:三个判定方法+一个公理推论(共四种)
(3)平行线间的距离
定义 :两条平行线中,任意一条直线上的所有点到另一条直线的距离都是一个定值,这个定值叫做这两天平行线间的距离。
性质 :平行线间的距离处处相等。
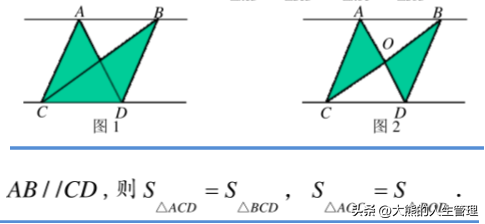
应用 :